第 0 章 预备知识
常用不等式¶
-
三角不等式:\(||a|-|b||\leq |a+b|\leq |a|+|b|\)
-
伯努利不等式:\((1+a)^n\geq 1+na\),其中 \(n\in\mathbb N^*,a\geq -1\)
-
均值不等式:
平方平均值 \(Q_n=\sqrt{\frac{a_1^2+a_2^2+\cdots+a_n^2}{n}}\) \(\geq\) 算术平均值 \(A_n=\frac{a_1+a_2+\cdots+a_n}{n}\) \(\geq\) 几何平均值 \(G_n=\sqrt[n]{a_1a_2\cdots a_n}\) \(\geq\) 调和平均值 \(H_n=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}}\),当且仅当 \(a_1=a_2=\cdots=a_n\) 取等。其中 \(a_i>0\)。
-
柯西不等式:
\((a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2)\geq(a_1b_1+a_2b_2+\cdots+a_nb_n)^2\),等号成立当且仅当 \(\exists \lambda,\mu\) 使得 \(\lambda a_i+\mu b_i=0\,(i=1,2,\cdots,n)\)。其中 \(a_i,b_i\in\mathbb R\)。
函数¶
-
\(f:X\to Y\):对 \(\forall x\in X\),存在唯一的 \(y=f(x)\in Y\)。\(Y\) 是陪域不是值域。定义域 \(D_f=X\),值域 \(R_f=\{f(x)\mid x\in X\}\),\(R_f\subseteq Y\)。\(y=f(x)\) 时,\(y\) 称为 \(x\) 的象,\(x\) 称为 \(y\) 的原象。
- 单射:每个 \(y\) 至多对应一个 \(x\)(不同 \(x\) 对应不同 \(y\))
- 满射:每个 \(y\) 至少对应一个的 \(x\)
- 双射:既是单射也是满射。\(x\) 与 \(y\) 一一对应
-
注意两个周期函数的和不一定是周期函数。
设 \(f(x),g(x)\) 分别是周期为 \(T_1>0,T_2>0\) 的周期函数,则 \(f(x)+g(x)\) 是周期函数 \(\Leftrightarrow\) \(\exists m\in\mathbb Q\) 使得 \(T_1=mT_2\),即两个周期函数的周期具有可比性。
反函数¶
- \(y=f(x)\) 与 \(x=f^{-1}(y)\) 图像重合。\(y=f(x)\) 与其反函数 \(y=f^{-1}(x)\) 的图像关于 \(y=x\) 对称。
三角函数¶
-
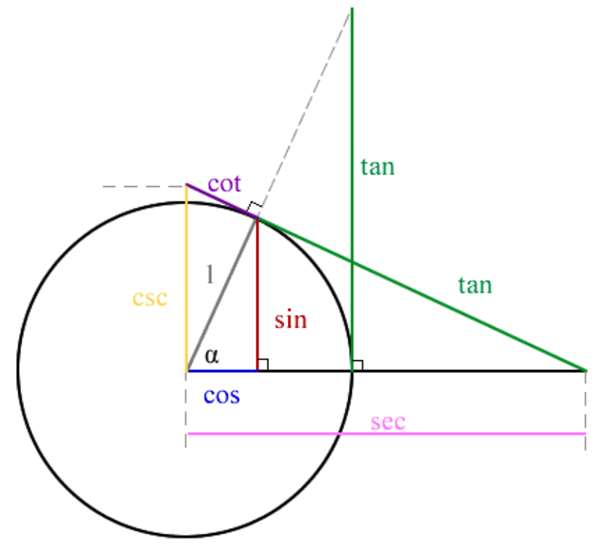
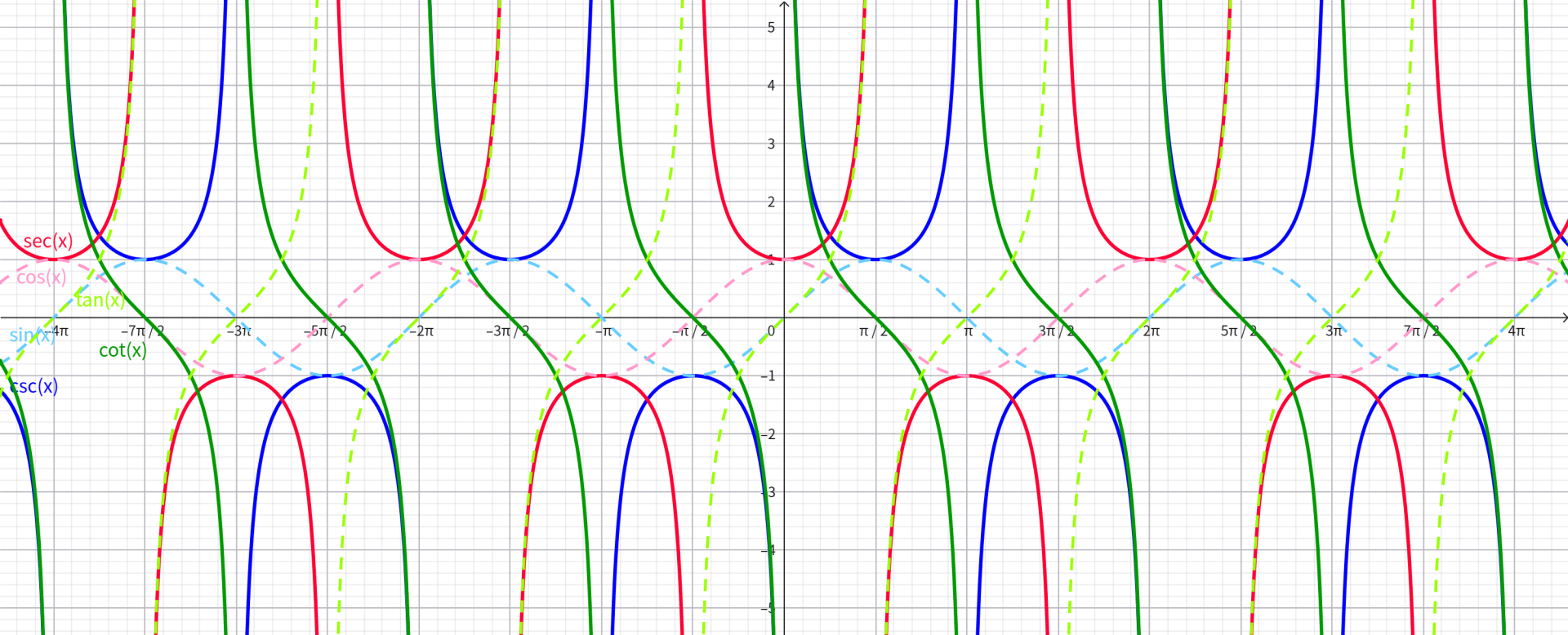
正弦函数 \(y=\sin x\)(sine)
余弦函数 \(y=\cos x\)(cosine)
正切函数 \(y=\tan x=\frac{\sin x}{\cos x}\,(x\neq k\pi+\frac{\pi}2,k\in \mathbb Z)\)(tangent)
余切函数 \(f(x)=\cot x=\frac{\cos x}{\sin x}\,(x\neq k\pi,k\in\mathbb Z)\)(cotangent)
正割函数 \(y=\sec x=\frac{1}{\cos x}\,(x\neq k\pi+\frac{\pi}2,k\in\mathbb Z)\)(secant)
余割函数 \(y=\csc x=\frac{1}{\sin x}\,(x\neq k\pi,k\in\mathbb Z)\)(cosecant)
-
三角函数公式
-
平方关系
\(\sin^2 \alpha+\cos^2\alpha=1\)
\(\tan^2\alpha+1=\sec^2\alpha\)
\(1+\cot^2\alpha=\csc^2\alpha\)
-
余角公式
\(\sin\theta=\cos(\frac{\pi}2-\theta)\),\(\tan\theta=\cot(\frac{\pi}2-\theta)\),\(\sec x=\csc(\frac{\pi}2-\theta)\)
-
倍角公式与半角公式
\(\sin 2\alpha=2\sin\alpha\cos\alpha\)
\(\cos 2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha=\cos^2\alpha-\sin^2\alpha\)
\(\sin\frac{\alpha}2=\pm\sqrt{\frac{1-\cos\alpha}2}\)
\(\cos\frac{\alpha}2=\pm\sqrt{\frac{1+\cos\alpha}2}\)
\(\tan\frac{\alpha}2=\pm\sqrt{\frac{1-\cos \alpha}{1+\cos\alpha}}=\frac{1-\cos\alpha}{\sin \alpha}=\frac{\sin\alpha}{1+\cos\alpha}\)
-
三倍角公式
\(\sin 3\alpha=3\sin\alpha-4\sin^3\alpha\)
\(\cos 3\alpha=4\cos^3\alpha-3\cos\alpha\)
\(\tan 3\alpha=\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}=\tan\alpha\tan(\frac{\pi}3+\alpha)\tan(\frac{\pi}3-\alpha)\)
\(\cot 3\alpha=\frac{-3\cot\alpha+\cot^3\alpha}{3\cot^2\alpha-1}\)
-
和差化积公式
\(\sin \alpha + \sin \beta = 2\sin \frac{\alpha + \beta}{2} \cos \frac{\alpha - \beta}{2}\)
\(\sin \alpha - \sin \beta = 2\cos \frac{\alpha + \beta}{2} \sin \frac{\alpha - \beta}{2}\)
\(\cos \alpha + \cos \beta = 2\cos \frac{\alpha + \beta}{2} \cos \frac{\alpha - \beta}{2}\)
\(\cos \alpha - \cos \beta = -2\sin \frac{\alpha + \beta}{2} \sin \frac{\alpha - \beta}{2}\)
-
积化和差公式
\(\sin \alpha \cos \beta = \frac{1}{2}[\sin(\alpha + \beta) + \sin(\alpha - \beta)]\)
\(\cos \alpha \sin \beta = \frac{1}{2}[\sin(\alpha + \beta) - \sin(\alpha - \beta)]\)
\(\cos \alpha \cos \beta = \frac{1}{2}[\cos(\alpha + \beta) + \cos(\alpha - \beta)]\)
\(\sin \alpha \sin \beta = -\frac{1}{2}[\cos(\alpha + \beta) - \cos(\alpha - \beta)]\)
-
万能公式
\(\sin \alpha = \frac{2\tan \frac{\alpha}{2}}{1 + \tan^2 \frac{\alpha}{2}}\),\(\cos \alpha = \frac{1 - \tan^2 \frac{\alpha}{2}}{1 + \tan^2 \frac{\alpha}{2}}\),\(\tan \alpha=\frac{2\tan\frac{\alpha}2}{1-\tan^2\frac{\alpha}2}\)
-
反三角函数¶
-
反三角函数的定义
Abstract
三角函数不是从定义域到值域的一一映射,不存在反函数。但是若将定义域限定在某个区间上,使得构成定义域到值域的一一映射,就能存在反函数了。
反三角函数没有周期性!
反正弦函数:\(y=\arcsin x:[-1,1]\to [-\frac{\pi}2,\frac{\pi}2]\),是奇函数。【\(\sin(\arcsin a)=a\,(a\in[-1,1])\),\(\arcsin(\sin a)=a\,(a\in[-\frac{\pi}2,\frac{\pi}2])\)】
反余弦函数:\(y=\arccos x:[-1,1]\to[0,\pi]\),是非奇非偶函数。【\(\cos(\arccos a)=a\,(a\in[-1,1])\),\(\arccos(\cos a)=a\,(a\in[0,\pi])\)】
反正切函数:\(y=\arctan x:\mathbb R\to (-\frac{\pi}2,\frac{\pi}2)\),是奇函数。【\(\tan(\arctan a)=a\,(a\in\mathbb R)\),\(\arctan(\tan a)=a\,(a\in(-\frac{\pi}2,\frac{\pi}2))\)】
反余切函数:\(y=\text{arccot }x:\mathbb R\to(0,\pi)\),是非奇非偶函数。【\(\cot(\text{arccot }a)=a\,(a\in\mathbb R)\),\(\text{arccot}(\cot a)=a\,(a\in(0,\pi))\)】
\(\arctan x+\arctan y=\begin{cases}\arctan\frac{x+y}{1-xy}&(xy<1)\\ \pi+\arctan\frac{x+y}{1-xy}&(xy>1,x>0)\\ -\pi+\arctan\frac{x+y}{1-xy}&(xy>1,x<0)\end{cases}\)
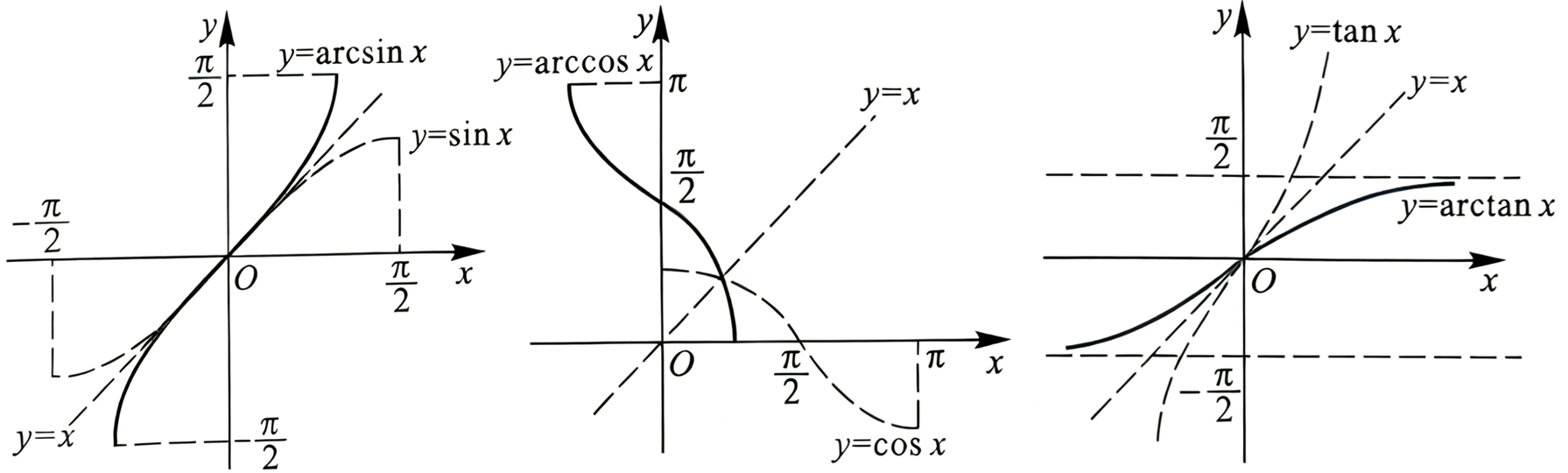

由上图知,当 \(x\in(0,1)\) 时,\(\sin x<x<\arcsin x\);当 \(x\in(0,\frac{\pi}2)\) 时,\(\arctan x<x<\tan x\)。
-
反三角函数之间的关系
-
\(\arcsin x+\arccos x=\frac{\pi }2\),\(|x|\leq 1\)
证明
法 1:
由于 \(\arccos x\in[0,\pi]\),所以 \(\frac{\pi}2-\arccos x\in[-\frac{\pi}2,\frac{\pi}2]\)。
\(x=\cos(\arccos x)=\sin(\frac{\pi}2-\arccos x)\),则 \(\arcsin x=\frac{\pi}2-\arccos x\)。
法 2:
令 \(\arcsin x=\alpha,\alpha\in(-\frac{\pi}2,\frac{\pi}2)\),有 \(\sin\alpha=x\)。
令 \(\arccos x=\beta,\beta\in(0,\pi)\),有 \(\cos\beta=x\)。
此时 \(\sin\alpha=\cos\beta\),即 \(\alpha+\beta=\frac{\pi}2\)(互余),得证。
-
\(\arctan x+\text{arccot }x=\frac{\pi }2\),\(x\in\mathbb R\)
证明
由于 \(\arctan x\in(-\dfrac{\pi}2,\dfrac{\pi}2)\),所以 \(\frac{\pi}2-\arctan x\in(0,\pi)\)。
\(x=\tan(\arctan x)=\cot(\frac{\pi}2-\arctan x)\),则 \(\text{arccot } x=\frac{\pi}2-\arctan x\)。
-
\(\arctan x+\arctan\frac 1 x=\begin{cases}\frac{\pi}2&(x>0)\\-\frac{\pi}2&(x<0)\end{cases}\)
-
\(\arctan\frac 1 x=\begin{cases}\text{arccot} x&(x>0)\\\text{arccot }x-\pi&(x<0)\end{cases}\)
-
\[ \begin{aligned} \arcsin x &=-\arcsin(-x)\\&=\frac{\pi}2-\arccos x\\ &=\arctan\frac{x}{\sqrt{1-x^2}}\,(|x|<1)\\ &= \begin{cases} \arccos\sqrt{1-x^2}&(0\leq x\leq 1)\\ -\arccos\sqrt{1-x^2}&(-1\leq x<0) \end{cases}\\ \arccos x &=\text{arccot }\frac{x}{\sqrt{1-x^2}}\,(|x|<1)\\ &=\begin{cases} \arctan\frac{\sqrt{1-x^2}}{x}&(0<x\leq 1)\\ \pi+\arctan\frac{\sqrt{1-x^2}}{x}&(-1\leq x<0) \end{cases}\\ &= \begin{cases} \arcsin\sqrt{1-x^2}&(0\leq x\leq 1)\\ \pi-\arcsin\sqrt{1-x^2}&(-1\leq x<0) \end{cases}\\ \arctan x &=-\arctan(-x)\\ &=\frac{\pi}2-\text{arccot }x\\ &=\arcsin\frac{x}{\sqrt{1+x^2}}\\ &=\begin{cases}\arccos\frac{1}{\sqrt{1+x^2}}&(x\geq 0)\\-\arccos\frac{1}{\sqrt{1+x^2}}&(x<0)\end{cases}\\ &=\begin{cases}\text{arccot }\frac 1 x&(x>0)\\-\text{arccot }\frac 1 x&(x<0)\end{cases} \end{aligned} \]
-
-
反三角函数的反三角运算
\(y=\arcsin(\sin x)\) 是 \(T=2\pi\) 的周期函数,且 \(\arcsin(\sin x)=\begin{cases}x&(-\frac{\pi}2\leq x\leq \frac{\pi}2)\\\pi-x&(\frac{\pi}2<x\leq \frac{3\pi}2)\end{cases}\)。
\(y=\arccos(\cos x)\) 是 \(T=2\pi\) 的周期函数,且 \(\arccos(\cos x)=\begin{cases}x&(0\leq x\leq \pi)\\-x&(-\pi\leq x<0)\end{cases}\)。
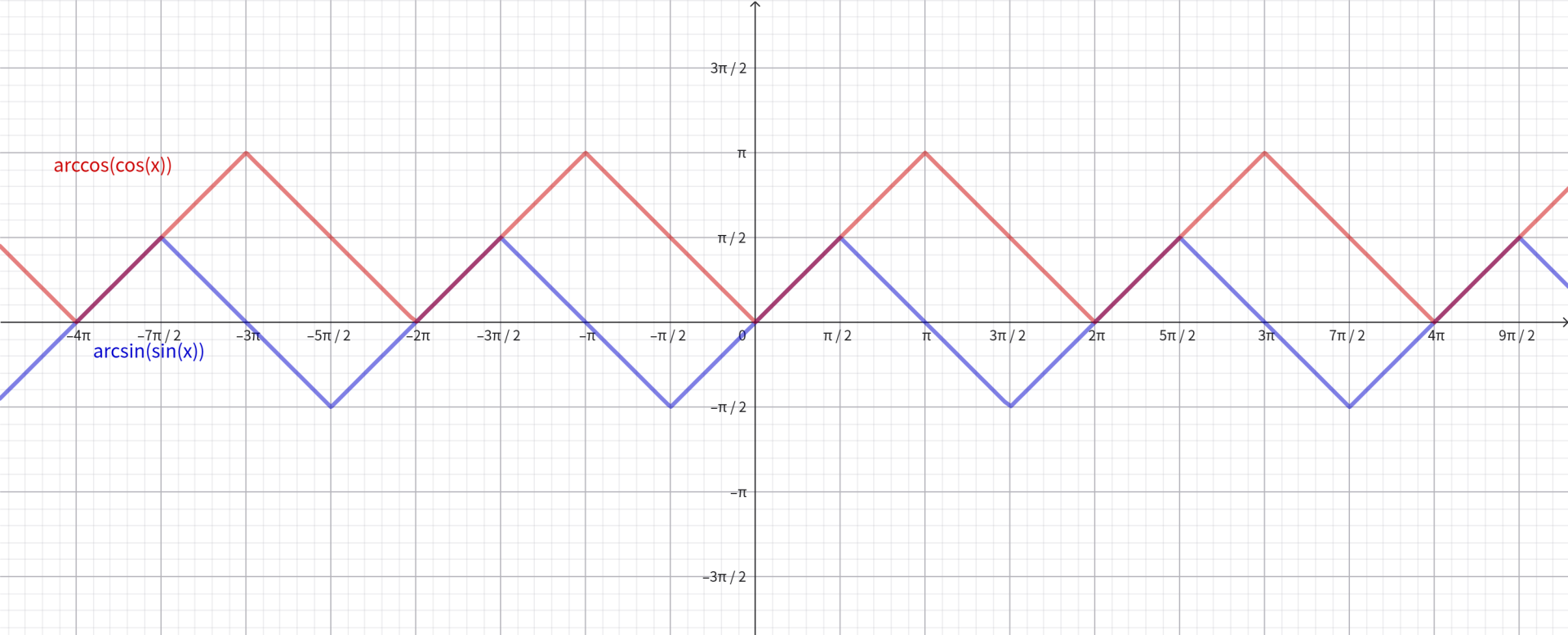
\(y=\arctan(\tan x)\) 是 \(T=\pi\) 的周期函数,且 \(\arctan(\tan x)=x\,(-\frac{\pi}2<x<\frac{\pi}2)\)。

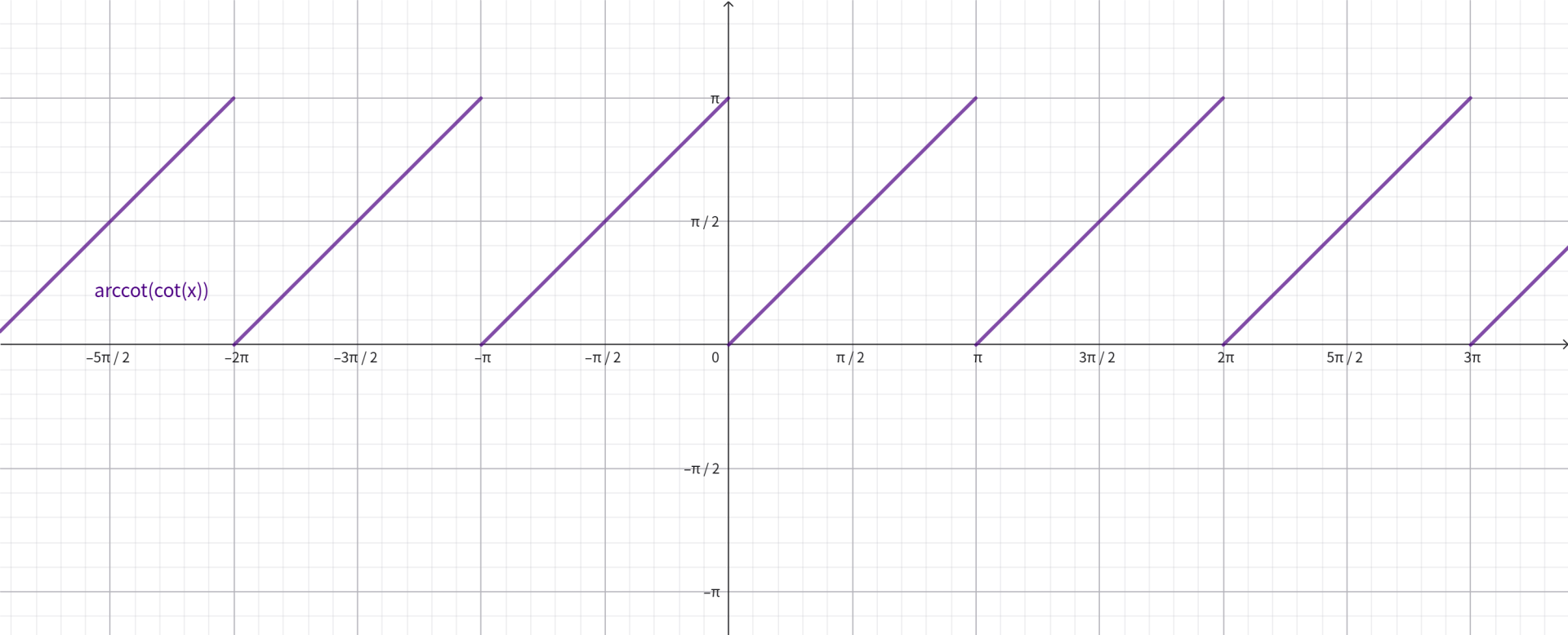
\(y=\text{arccot}(\tan x)\) 是 \(T=\pi\) 的周期函数,且 \(\text{arccot}(\cot x)=x\,(0<x<\pi)\)。
复数¶
-
欧拉公式 \(e^{ix}=\cos x+i\sin x\)
\(\cos x=\frac{e^{ix}+e^{-ix}}{2}\),\(\sin x=\frac{e^{ix}-e^{-ix}}{2}\)
-
练习
例题
计算:\(\arcsin\dfrac{1}{\sqrt{10}}+\arccos\dfrac 7{\sqrt{50}}+\arctan\dfrac{7}{31}+\text{arccot }10\)。
解答
\(\arcsin\dfrac{1}{\sqrt{10}},\arccos\dfrac 7{\sqrt{50}},\arctan\dfrac{7}{31},\text{arccot }10\) 分别是复数 \(3+i,7+i,31+7i,10+i\) 的辐角,且均为锐角。故 \(I\) 为复数 \((3+i)(7+i)(31+7i)(10+i)\) 的主幅角。
\(I=\arg((3+i)(7+i)(31+7i)(10+i))=\arg((20+10i)(303+101i))=\arg 1010(2+i)(3+i)=\arg(5050(1+i))=\dfrac{\pi}4\)
双曲函数¶
-
双曲正弦 \(\sinh x=\frac{e^x-e^{-x}}{2}\)
双曲余弦 \(\cosh x=\frac{e^x+e^{-x}}2\)
双曲正切 \(\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)
双曲余切 \(\coth x=\frac{e^x+e^{-x}}{e^x-e^{-x}}\)
反双曲正弦 \(y=\text{arcsinh }x\)(实际上等于 \(\ln(x+\sqrt{x^2+1})\))
反双曲余弦 \(y=\text{arccosh }x\)(等于 \(\ln(x+\sqrt{x^2-1})\))
反双曲正切 \(y=\text{arctanh }x\)(等于 \(\frac 1 2\ln\frac{1+x}{1-x}\))